格林威治CFD计算方法介绍¶
控制方程¶
风资源评估需要对复杂地形下的大气边界层进行数值模拟,来得到某一地区内的风资源分布情况。由于实际大气边界层内的流动机理十分复杂,工程上多采用计算流体力学(CFD)的方法进行计算。根据某一控制体内的质量守恒和动量守恒,假设大气为不可压缩流体。可以得到流体力学的控制方程:
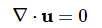
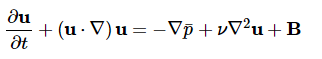
其中:U=(u,v,w), p=p/rho0, nu为运动学粘性系数,B为体积力项,如柯氏力等。若需进一步考虑大气热稳定度影响,则需要引入温度(位温,theta)方程:
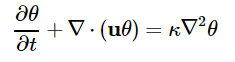
RANS(雷诺平均)方法介绍¶
风资源评估多考虑的是20年平均意义下风电场内的风况,因此,可以采用雷诺平均方法(RANS)进行计算。为此,我们将变量U分解为平均量(ū)和脉动量(u’),进而可以得到如下方程:
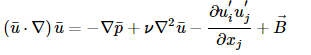
其中,为雷诺应力项,根据Boussinesq的涡粘理论假设,可以得到如下关系:
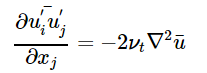
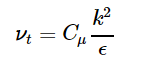
为此,我们采用两方程模型对湍动能(k)和湍流耗散率(epsilon)的进行求解,来实现方程的封闭:
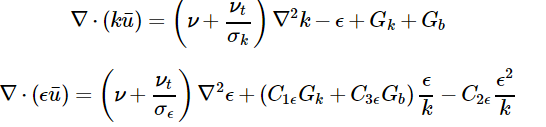
其中Gk为湍动能生成项,Gb为考虑大气热稳定度情况下的湍动能生成项。C1、C2、C3、Sigmak和SigmaEps为湍流模型常数。在不考虑大气热稳定度效应时,Gb=0。通常,C1=0.09,C2=1.92,SigmaK=1.0, SigmaEps=1.1111。
格林威治CFD介绍¶
格林威治CFD采用中性大气下的RANS方法,来实现风电场的CFD计算。其主流模块为中性大气下的RANS计算方法;同时我们还开发了考虑热稳定度的RANS方法和适用于复杂风电场的非稳态混合大涡模拟方法等。
根据中性大气边界层的假设,入口边界可采用对数风廓线:
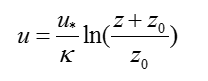
其中,z0为地表粗糙度;kappa为冯卡门常数,通常取为0.41;Ustar为摩擦速度。计算中可以通过设置参考高度(如100m)下的参考风速(如8m/s)和当地的地表粗糙度得到摩擦速度的大小,进而得到入口风廓线的形状。在考虑大气热稳定度效应时,我们通过给定的Monin-Obukhov长度和具体的项目位置,进行一维的CFD计算,得到当地实际的风廓线形状。出口边界采用零压力梯度边界条件。地面采用无滑移边界条件。
为保证计算精度,需要控制网格的质量,并同时应尽量保证网格与地面正交。为此,我们开发了网格生成算法,并通过参数优化,实现了在复杂地形下的高质量网格的自动化生成。针对实际风电场项目,网格范围多为20kmX20km,垂直高度为3km-7km。通过网格收敛性的研究发现,针对实际风电场项目,水平网格分辨率应小于25m;垂直方向第一层网格高度为2m,叶轮面范围内垂直网格分辨率为5m-7m左右。
RANS计算我们采用SIMPLE算法,并严格控制残差的收敛,计算收敛准则如下:全场U的残差需小于3E-5,湍动能的残差需小于2.5E-6。